The Struggle Is Real: Productive Struggle

Learning By Doing

Let's get this party started with a fun little puzzle. You may have seen this on your favorite social media platform [1]. 

See if you can solve it.

Struggling Productively

That was a difficult problem, right? Would you say you "struggled" while attempting to solve it? I know I did! This experience raises a couple of questions:

1. What, exactly, causes us to struggle?

2. When does struggling assist learning, and when does it harm learning? 

3. Under what conditions does struggling lead to long-term learning and transfer? 

Before we attempt to answer these questions, let's acknowledge the emotional components of struggling. I can only speak for myself, but phenomenologically, it doesn't always feel great. I get hot. I feel dumb. Intrusive thoughts distract me from the task-at-hand. Of course, if your working memory is loaded with these intrusive thoughts, then you have fewer resources to dedicate to the current task...which will ultimately cause you to fail!

Sources of Struggle

What causes us to struggle? 

Prior Knowledge: First, we may not have all of the prerequisite knowledge to solve the problem. Once we recognize this fact (hopefully earlier rather than later!), then we can treat it as a quest to find the missing information. 

Incorrect Assumptions: Another reason why we might struggle is because we've made an incorrect assumption. If you assume that a fox and wolf weigh the same, then you will eventually run into a road-block when solving the above problem. 

Unnecessary Problem Constraints: We might struggle because we imposed an unnecessary constraint on the problem. This often happens while solving an insight problem. For example, in the classic nine-dot problem, problem solvers unnecessarily add the constraint that they are not allowed to go beyond the edge of the box. 

Flawed Representation: Finally, we may have chosen a flawed or limited representation. We've seen time and again how important representations are for solving problems. For example, students fail to calculate the area of a parallelogram when presented outside of the canonical orientation (i.e., laying flat along the long side).

What makes struggling "productive?"

According to James Hiebert and Douglas Grouws's book chapter [2], productive struggle happens when a student is working on a problem just outside of their current ability level. This is related to Lev Vygotsky's idea of the "zone of proximal development" (see Fig. 1). 

There are things that you can do autonomously. These are well-practiced skills or declarative knowledge that you've mastered previously. There is also a bunch of things you can't do (at least not yet!). But in between those two spheres are things that you can do with some assistance.

Struggle is most productive when done under the watchful eye of a more knowledgeable partner. They are there to step in and nudge the novice in the right direction. 

Figure 1. Vygotsky's three zones, with the middle as the "zone of proximal development."

Struggle, then, is maximally helpful for several reasons. 

It allows students to appreciate the context of the lesson. If you just give a lecture on solving systems of equations, then the student may not have any appreciation for why systems of equations is a powerful problem-solving technique. However, if you first let them try to figure out how to calculate the weight of the chicken, fox, and wolf, then they might see the utility of systems of equations.

If a student is lacking a key piece of information, then struggling to solve a problem may expose a gap in their knowledge. An impasse in problem solving might force a student to confront the possibility that there is something wrong with their understanding [3]. 

There may be some small amount of discovery involved. For example, there are are (at least) three key insights when solving this animal weight problem: using variables (x, y, & z) instead of animals, isolating a variable for each of the three known weights, and finally substituting the isolated variables into the other equations. Having a key insight or making a discovery is highly motivating.

That brings us to the final reason. Struggle is useful because it necessarily engages a student's conceptual understanding. For any of the three key insights, there is a rich conversation that can connect back to knowledge that a student already possesses (e.g., the concept of a "variable," isolating a variable, variable substitution, and mathematical equivalence). 

The Classroom Connection

Struggling doesn't have to be fraught with negative emotions. In some contexts, struggling is actually kind of fun. Think about the last video game you played. Games are specifically designed to cause you to struggle. In fact, there is some research to suggest that players actually enjoy dying (the ultimate failure!) in first-person shooter games more than shooting other players [4]. Another example is a well-written mystery. You may struggle to figure out "who dun it," but it is an entirely enjoyable experience. It would be beneficial to everyone if academic tasks that cause us to struggle to be structured in a way that is more like a game, puzzle, or mystery. 

Perhaps our struggle as educators and instructional designers, is to figure out how to make struggling an enjoyable educational experience! 🧩


Share and Enjoy!

Dr. Bob

Going Beyond the Information Given

[1] I adapted this problem from Sara Van Der Werf's blog, and you can follow her on twitter @saravdwerf. This might also be a good time to link back to our prior conversation about problem isomorphs.

[2] Hiebert, J., & Grouws, D. A. (2007). The effects of classroom mathematics teaching on students’ learning. Second handbook of research on mathematics teaching and learning, 371-404.

[3] VanLehn, K. (1988). Toward a theory of impasse-driven learning. In Learning issues for intelligent tutoring systems (pp. 19-41). Springer, New York, NY.

[4] Ravaja, N., Turpeinen, M., Saari, T., Puttonen, S., & Keltikangas-Järvinen, L. (2008). The psychophysiology of James Bond: Phasic emotional responses to violent video game events. Emotion, 8(1), 114-120. https://doi.org/10.1037/1528-3542.8.1.114

Twenty Thousand Leagues: Depth of Processing

Learning By Doing

Without cheating, take a moment to scan the following matrix of pennies. 

Which drawing represents the current design of a penny? (Fun fact: the front-side of a coin is called the obverse.)

Figure 1. Can the real penny please stand up?

Once you've made your selection, reflect on the following questions:

1. Was this a difficult task?
2. If so, why was this difficult?
3. If not, what life experience did you have that prepared you to answer quickly and accurately?

Like a Bad Penny...

I've used the penny demonstration in several groups over the past year, and I would estimate that about 1 in 30 select the right coin [1]; therefore, it's likely this task was hard for you, too. The question is why (despite the fact we've all seen a penny many, many times)? 

One reason is related to the first of three processes in our simple model of memory: encoding. You might be unable to identify the real penny, in a sea of distractors, because you never encoded the specific properties of a penny. 

On the other hand, you probably did encode the approximate size, the edge's smoothness, the inclusion of our 16th president, and the copper veneer. You encoded those properties because they help you meet your learning goal: to spend a penny. You need to differentiate a penny from a nickel, dime, and quarter. In other words, learning is goal oriented. If your goal changes (e.g., you need to accurately draw a penny for your blog), then you will encode those specific details.

That's Deep.

Misidentifying a penny among 14 distractors is a pretty powerful example of encoding failure. We've all seen a penny before, but it's unlikely that someone quizzed you on the specific features. So what if they did? Is there a way to enhance our ability to remember something over the long haul? In other words, is all processing is equally effective? I'm sure the answer is obvious to you. But what's the evidence?

To test if different levels of processing lead to better (or worse) memories, two very famous memory researchers, Fergus Craik and Endel Tulving, conducted a series of experiments [2]. They asked volunteers to come to their lab and study a list of words. They experimentally manipulated how deeply the participants studied the words across five levels of processing. They asked the participants (1) if the word was present; (2) if the word was written in capital letters; (3) if the word rhymed with another word; (4) if it was in a specific category;  or (5) if it fit into a given sentence. Table 1 contains both positive and negative examples for the word honey.

Table 1. The experimental manipulation of processing depth. 

Level of Processing	Positive Example	Negative Example
1. Is there a word present?	HONEY
2. Is the word in capital letters?	HONEY	honey
3. Does the word rhyme with ___?	funny	monk
4. Is the word in a category of ___?	a type of food	a part of a ship
5. Does the word fit in this sentence: ___?	He eats ______ on his toast.	She met a ____ on the street.

Before you look at the results, what do you predict they found? Does processing a word at a deeper, more semantic level, lead to better memory trace? Or is processing all the same, as long as it passes through the attentional system and into working memory? 

Here's what they found: 

Figure 2. Memory accuracy as a function of depth of processing.

According to their results, there is a huge advantage for processing a word at a deeper, semantic level. 

The Classroom Connection

The evidence from Craik and Tulving's study is highly suggestive. As educators, we want our students to process the information we want them to learn as deeply as possible. This advice is consistent with other research on memory:

1. We saw evidence that generating a to-be-remembered item can also have beneficial effects on long-term recall. 
2. Research on retrieval practice demonstrated that rereading notes or a chapter summary was a terrible way to study. Instead, students should engage in an effortful attempt to retrieve the information from memory. 
3. We also reviewed a study that showed students prefer easy hints to more difficult hints when self-testing. Unfortunately, their preferences ran completely counter to the empirical evidence suggesting that more effortful retrieval leads to better retention. 

Because encoding is a vitally important step for robust learning, it is helpful to understand what the empirical data has to say: The deeper the processing, the longer lasting the memory. 

Process that as deeply as you can! 🦑

Share and Enjoy!

Dr. Bob

Going Beyond the Information Given

[1] By the way, the right answer is (a). Don't believe me? I bet the US Mint will back me up.

[2] Craik, F. I., & Tulving, E. (1975). Depth of processing and the retention of words in episodic memory. Journal of experimental Psychology: General, 104(3), 268.

How To Grow a Third Arm: Neuroplasticity, Synaptic Pruning, & Myelination

Learning By Doing

It's amazing —stunning, actually — how quickly the brain can adapt. A really wild example of the brain's adaptivity is growing a third arm. You can actually do this at home [1]. To grow a third arm, you will need the following supplies: 

1. An accomplice 
2. A rubber hand
3. A small brush
4. A blanket or towel
5. A very sharp knife or hammer

First, place your real hand and the rubber hand next to each other. Then, cover up your arm with the blanket so only the hands are visible. Then, have your accomplice use the small brush to stroke both the real and fake hand at the same time. Do this for a minute. This step is crucial because you are creating a conflict in the brain that it must eventually resolve. In the final step, have your accomplice threaten the rubber hand with the knife or hammer. If the brain successfully completes the remapping, then you will withdraw your real hand because your mind has taken ownership of the fake hand [2]!

The Adaptive Brain

The "rubber hand illusion" isn't just a fun parlor trick to play with your friends at Halloween. Neuroscientists have figured out how get people to rewire their brains so they can control a third robotic arm [3].

These stunning demonstrations show how remarkably adaptable and resilient the brain is. This adaptivity is analogous to the mechanism the mind uses after suffering a trauma. For example, if a specific region of the brain is damaged, then it has some capability to accommodate that trauma. In extreme cases, the brain will adapt by overtaking adjacent tissue so the individual can regain some of their original functionality. 

What are the specific neural mechanisms for these adaptations, and what are some real-life implications?

Adaptivity and Late Bloomers

In a previous post, we learned that executive functioning (EF) is situated in the pre-frontal cortex (i.e., part of the brain just behind the forehead). Given its centrality to higher-order thinking, it is surprising to learn how late executive functioning develops. During young adulthood, the brain undergoes two important processes: synaptic pruning and myelination. 

Synaptic pruning sounds horrifying, but it is a necessary process whereby unnecessary synapses (i.e., the connections between neurons) are removed. 

Myelination is the process of adding a layer of lipids (or fat) to the outside neuron. The purpose of myelin is to speed up neural transmission. It's analogous to adding insulation to an electrical wire.

By most estimates, the frontal cortex isn't fully myelinated until a person reaches 25 years of age. That might explain why teenagers and young adults don't always make the best decisions. Their brain is still developing in the most critical region for planning, organization, response suppression, and (perhaps most importantly) counterfactual thinking! 

The Classroom Connection

Understanding the timeline for neural development also has an important implication for education. Some students are late bloomers and need extra time for their frontal lobe to fully develop [4]. To give these students the time they need, there should be some flexibility in their educational timeline. Taking a "gap year," traveling abroad, or enrolling in AmeriCorp might be precisely what these students need. Not all students should be expected to rush directly from high-school to college. 

In closing, we owe our brains a great debt of gratitude. Being adaptive and flexible is what makes us who we are. And who knows...maybe someday "being who we are," might include controlling a third arm. 💪

Share and Enjoy!

Dr. Bob

Going Beyond the Information Given

[1] The illusion of owning a third arm [link].

[2] Threatening a rubber hand that you feel is yours elicits a cortical anxiety response [link].

[3] Penaloza, C. I., & Nishio, S. (2018). BMI control of a third arm for multitasking. Science Robotics, 3(20).

[4] Karlgaard, R. (2019). Late Bloomers: The Hidden Strengths of Learning and Succeeding at Your Own Pace. Broadway Business.

Making Tests (More) Fun Through Hints Increases Student Uptake Of Self-Testing

LEARNING SCIENTISTS POSTS, FOR TEACHERS 

Editorial Note: I am extremely excited to share with you a cross-posting from a group of like-minded scientists. This post originally appeared on The Learning Scientists Blog. The Learning Scientists aim to make research on the science of learning more accessible. Take it away, Dr. Carolina Kuepper-Tetzel!

By Carolina Kuepper-Tetzel

There is plenty of research supporting retrieval practice as a learning strategy. If left to their own devices, students report using self-testing as a way to assess how much they know, but not as a learning strategy per se (1). However, self-quizzing is a valuable learning strategy and more effective than other strategies preferred by students like ‘rereading chapters and notes’. In a recent series of experiments Vaughn and Kornell (2) investigated factors of test characteristics that may be conducive in motivating students to use self-testing as a primary strategy. They started with the assumption that, in general, students enjoy being tested – as long as they feel that they can get the answer right. Thus, increasing the likelihood of getting the correct answer will sway students to choose self-testing over simple restudying.

Image from Pixabay

How did the authors investigate this idea? 

They set up an experiment and had participants study 60 unrelated cue-target word pairs (e.g., ‘town-scones’). After the first study round, participants were given the option to choose how they would like to continue studying each word pair. So, before each word pair was shown to them they could pick between four options, i.e., 0-letter target (‘town-______’), 2-letter target (‘town-s____s’), 4-letter target (town-sc__es), or 6-letter target (‘town-scones’). Target words were always presented on the right side of the word pair and always consisted of 6-letter words. Thus, the 6-letter target condition was essentially a restudy condition that did not involve retrieval practice. The other three conditions all involved retrieval practice of the target word to some extent – with less or more hints. The authors were interested to see which of the four options students would pick for each study trial. The graph below shows the result.

Figure from Vaughn and Kornell (1)

As you can see: Students picked the 4-letter option more often than any of the other options. Furthermore, students reported that the 4-letter option was “the most fun” with 71% agreement for that option compared to only 11% agreement for the 6-letter option. Interestingly, the 0-letter option received an agreement score of 0% (the 2-letter option a score of 17%). So, it seems to be the case that pure retrieval practice without hints rules self-testing out as a strategy that students would select. Consequently, providing some hints can make self-testing more enjoyable and make students select it more often when they are given the choice.

They followed up their first experiment with a second one where they only included the two extreme options for participants to choose from: 0-letter versus 6-letter option. They found that students went for the pure restudy (6-letter) option in approximately 80% of the trails versus 20% for the pure retrieval practice option (0-letter). This shows that a self-testing option that offers no hints is perceived as an unattractive option and in such a scenario, students will go for restudying as a strategy.

After establishing student preference for testing with hints, it is important to see if that kind of self-testing is actually beneficial for performance on a final test. In follow-up experiments, the authors showed that indeed all three retrieval practice options – independent of hint level (i.e., 0-, 2-, 4-letter) – increased performance on a final test given two minutes later; more than the pure restudy condition (6-letter). However, one important caveat seems to be to make sure that students actually engage in retrieval processes, i.e., actually retrieve information from memory. If, for instance, the word pairs allowed correct guessing of the target word given the cue word – instead of retrieval – providing more hints led to detrimental effects of performance.

Image from Pixabay

Where does this leave us? 

Motivating students to change their habits on what strategies they use is not an easy task. However, it seems to be worthwhile thinking about ways to restructure or redefine the learning environment or task characteristics in a way that changes student perception of it towards higher attractiveness and more fun. Providing hints strategically can be one way to achieve this. It increases the likelihood to get the answer right which presumably increases the positive emotions associated with it and leads students to adopt self-testing in the future. As with all implementation tips, it is crucial that the underlying cognitive processes for the benefit of self-testing is triggered in the student. For the case here: Students still need to engage in retrieval of the material and not just rely on guessing to get the answer right.

References:

(1) Morehead, K., Rhodes, M. G., & DeLozier, S. (2016). Instructor and student knowledge of study strategies. Memory, 24, 257–271.

(2) Vaughn, K. E., & Kornell, N. (2019). How to activate students’ natural desire to test themselves. Cognitive Research: Principles and implications, 4, 1-16.

Minding the Gap: Connecting teachers and students to learning science

Editorial Note. We are in for a real treat! We have a guest post by Josh Ling, the CEO and founder of Podsie. I'm a fan of Podsie because it is one of the rare ed-tech companies that takes learning science seriously and attempts to fix a rather significant problem in learning and teaching. Take it away, Josh!

Learning By Doing

 

Let’s start by doing a challenge. (Full disclosure: if you end up not finding this exercise challenging, it’s because I typically do this with middle-school students!)

Here we go:

1. Google a map of North Africa. Then, study the country that’s to the west of Egypt for 10 seconds. Next, study the country that’s south of Egypt for 10 seconds.

2. Close that tab!

3. Count to 20.

4. Now, test yourself. Are you able to recall the names of the countries to the west and to the south of Egypt?

Given the short duration of time that passed between you learning the names and then being quizzed, you were likely successful in getting them both right! However, what if I asked you to retrieve that same information again in 3 hours? How about tomorrow? Or in a week? Or in a month?

“Hoping to find some old forgotten words…” —Africa, Toto

At this point, you might have realized that we’re revisiting some topics that have previously been discussed on this blog: forgetting and how one might combat it.

In those posts, Dr. Bob explained:

“Forgetting is non-linear, meaning it decays quickly and eventually slows down.”

Visually, he also provided a forgetting curve that shows how fast we forget newly learned information:

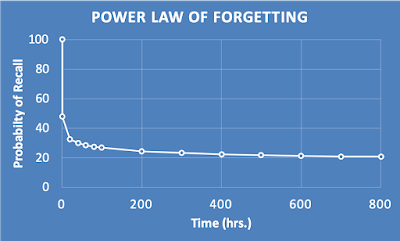
The good news is that we can combat this forgetting through retrieval practice, where recalling that information from memory strengthens the stickiness of that information and slows the rate of forgetting. 

To take it one step further, those blog posts referenced another article from Duolingo’s blog that expanded on the optimal cadence for retrieval practice. At Duolingo, they utilize the spacing effect [1], and they use their vast amounts of data points to map out a model of when students should review certain vocabulary words based on their prior performance [2]: 

Research shows that the optimal time to retrieve information is right when you’re about to forget it [3]. Because each retrieval practice should increase the durability of that memory, the retrieval practice is spaced out with longer and longer lag times in between each session. Practically, this has the positive effect of increasing studying efficiency because at any given moment, you can focus only on the subset of content you’re most about to forget.

The Classroom Connection

I taught 8th grade math for two years from 2013 - 2015.

As a first year teacher, I was overly focused on just making it through the large amount of content that was mandated by our state curriculum. I gave little time or thought to review, and overall, my classroom looked a lot like the one that Dr. Bob described:

“The traditional method of teaching is to introduce a topic, solve a few illustrative problems that relate to that topic in class, assign some homework problems, and then give a test a few days or weeks later to see if the students retained the material. For highly important topics, the same items might make a reappearance on the final exam.”

Dr. Bob also describes the problem with this traditional approach:

“...if a topic hasn't been discussed in several weeks, then it is likely the memory system is going to treat that memory as unimportant, and it will find itself on the fast side of the forgetting curve. Second, if too much time elapses between the presentation and evaluation, then the probability of successful recall is going to be very low.”

I had never heard of the forgetting curve, but I saw it working in full force with my students.

In my second year, I resolved to provide more review opportunities. Overall, however, I was still completely ignorant to the basic principles of learning science. I didn’t know that retrieval was the most effective way to review. When I myself was a student, I was a serial crammer, so the spacing effect was basically foreign to me.

As a result, review in my classroom was often suboptimal. For example, I occasionally asked my students to just re-read their notes. I would sometimes put questions covering older topics on students’ homeworks or quizzes, but certainly not with enough consistency to make it stick. To make matters worse, it was a massive challenge to figure out which topics most needed review. Some of my students needed to review fractions at certain points of the school year, while others really needed to review solving integer operations. 

That year, my students performed better than the previous year, but continued to struggle to effectively retain information that they had learned. 

A few years later

A couple years later, I made a career change and became a software developer. Around that time, I read a book called Make it Stick by Roedinger, McDaniel, and Brown [4], and I was blown away.

This book was the first time that I learned about the basics of learning science. The book went through the nuances of how we learn and retain information, and it provided definitive recommendations on research-backed practices that educators should be using in their classrooms, like retrieval and spacing.

My mind immediately flashed back to my classroom, where these best practices could have made a substantial difference with how my students learned. I also realized that this issue went further than just my own classroom. By that point, I had sat through countless hours of teacher professional development, and I also had a master’s degree in education. However, not once did we cover those basic cognitive science principles on how students learn.

Now

Those experiences were the inspiration for Podsie, a nonprofit edtech I co-founded that’s focused on improving student learning and empowering teachers by making the science of learning more accessible.

At Podsie, we’ve built an online web app for teachers and students that makes best practices like spacing, retrieval, and interleaving easy to implement in the classroom. With Podsie, a teacher creates an assignment that assesses the content that students learned. When students complete a question on an assignment, the question goes into that student's personal deck, which essentially represents the entire body of knowledge that a student should know for that class.

Each student's personal deck is powered by a spacing algorithm that determines when the student should review a question again, similar to how Duolingo prompts students to review a vocab word when they are just about to forget it. Overall, this ensures that students have a personalized review experience that allows them to focus on concepts they most need to review.

All in all, we are incredibly excited to make it easier for teachers and students to utilize and learn more about learning science best practices. On the way, we’ve had the privilege of learning from and working with cognitive scientists like Dr. Bob who are on the same journey to ensure students and educators can be the best they can be.

We launched a beta trial of our app in August of 2020, and we’re preparing to launch in June of 2021. Our app is free for teachers and students, and if you’re interested, you can sign up on www.podsie.org to be notified as soon as we’re live!

Going Beyond the Information Given

[1] Cepeda, N. J., Pashler, H., Vul, E., Wixted, J. T., & Rohrer, D. (2006). Distributed practice in verbal recall tasks: A review and quantitative synthesis. Psychological bulletin, 132(3), 354.

[2] Figure 3 is taken from https://blog.duolingo.com/how-we-learn-how-you-learn/, which was originally published in their academic paper: 

Settles, B., & Meeder, B. (2016, August). A trainable spaced repetition model for language learning. In Proceedings of the 54th annual meeting of the association for computational linguistics (volume 1: long papers) (pp. 1848-1858). 

[3] Landauer, T. K., & Bjork, R. A. (1978). Optimal rehearsal patterns and name learning. In M. M. Gruneberg, P. E. Morris, & R. N. Sykes (Eds.), Practical aspects of memory (pp. 625-632). London: Academic Press.

[4] Brown, P. C., Roediger III, H. L., & McDaniel, M. A. (2014). Make it stick. Harvard University Press.

The Mind’s CEO: Executive Function

Learning By Doing

Let's play a game. It's super fun...I promise! Download and print this file. Your goal is to cross out all of the lower case d's with two dots above it. Try to be as fast and accurate as possible. Don't forget to time yourself. Ready? Go! [1]

Back to the Front

Stop me if you've heard this one. The left hemisphere of your brain is responsible for logical processing; the right hemisphere is designed for creative and wholistic thinking. While there may be a tiny grain of truth to these over-generalizations, there is a much less talked about difference in brain functioning. As you go from the back of the brain to the front, thinking goes from extremely concrete to highly abstract. 

That's right! The very back of your brain is reserved for visual processing and low-level muscle control. But as you move forward, toward your forehead and eyes, thinking becomes much more complex. This is the location of higher-order thinking skills such as planning, organizing, and problem solving. This area of the brain called the pre-frontal cortex. This is where you will find executive functioning.

Executive function includes several different cognitive processes. They include, but are not limited to, working memory, response suppression, and attentional focus. 

Working Memory

Baddeley's model of working memory features three components (see Fig. 1). There are two slave systems — the visuospatial sketchpad and the articulatory loop — and a central executive. The central executive controls the operation of the slaves systems. It can store and retrieve information from each slave system, and it can also re-represent the same piece of information in different forms (e.g., translating a piece of an image into a word, or vice versa). 

In other words, the central executive must make decisions about the relevance of information and how best to represent it. It must also decide which information needs to be refreshed and maintained in working memory and which information can be safely discarded.

Figure 1. Baddeley's model of working memory.

Response Suppression

We all know how difficult it is for some people to suppress the urge to respond in certain situations. Below are several examples of response suppression, categorized by the domains in which they were found:

Popular Culture: Response suppression failure has made its way into movies (e.g., Roger Rabbit cannot contain himself when faced with the old "shave and a haircut trick") and games. In a previous post on Ironic Processing, we talked about the frustration inherit in the game of Taboo!.

Psychology: We also see examples of response suppression in the materials used in cognitive psychology. The Stroop task is a classic example because, in one variant of the task (i.e., when the color of ink and word conflict), you must suppress the urge to read the word and name the color of ink. 

Neuroscience: The frontal lobe (i.e., the seat of executive functioning), is responsible for response suppression. There is a really interesting example from neuroscience where Phineas Gage had his fontal lobe damaged. After his accident, he became something of a jerk. His behavior strongly suggested that he could not suppress his urges.

Classroom: Response suppression in the classroom is very real, and it can take on many different forms. Behaviorally, little kids (eventually) learn that they must raise their hand before blurting out the answer to the teacher's question. 

A more cognitive example can be found in the world's shortest IQ test: 

1. A bat and a ball cost $1.10 in total. The bat costs $1.00 more than the ball. How much does the ball cost? _____ cents

When confronted with a question like this, you may feel the need to suppress your intuitive answer (10 cents) and apply your knowledge of algebra to determine the answer ((b+100) + b = 110). In this case, the fast answer isn't the right answer [2].

Attentional Focus 

In a previous post, we talked about the "myth of multitasking." Most people think they can do multiple things at once, but there are severe limitations. You might be able to walk, talk, and chew gum, but you won't be able to listen to a lecture, deeply process the contents, and simultaneously take notes. People are serial processors (as opposed to "parallel processors"). A useful metaphor for attention is that it is a spotlight, and it can only shine on one thing at at time. 

As serial processors, we need to make decisions about which stimuli to pay attention to. This is where executive functioning comes into play. When an alert goes off on our phone, we have to decide to pay attention to it (or not). Unfortunately, that "decision" isn't really a decision anymore. Over time, we become conditioned to immediately abandon what we were thinking about and look at our phone. In other words, we have trained our attentional system to give our phone primary status. Ideally, we would structure our learning environment so that it removes unnecessary distractions. Keeping cellphones on "Do not disturb" mode and out of view is the best way to prevent our attention from being captured.

Attentional distraction can also be internally generated. For example, if you are a minority, and you are reminded of your minority status, perhaps because of an off-hand comment or some other feature in the environment (i.e., you are the only one of your group), then those distracting thoughts can pull attention away from the task at hand. This phenomenon is called stereotype threat, and it has pernicious effects on performance [1].

The final example of attentional focus is on information within a task. Suppose you are asked to solve the following problem: 

Derek has 4 action-adventure video games and 9 board games. Desi has 3 role-playing video games and 2 lawn games. If they combine their games, how many video games do Derek and Desi have? 

Notice that this problem has some very tempting, but completely irrelevant, information. One skill that students need to learn is to ignore the distracting information as they solve the problem. Some teachers might recommend highlighting the relevant information (or crossing out the irrelevant information). The goal is to help the attentional system stay focused on the relevant bits.

The Classroom Connection

How can we structure the classroom environment to support the development of executive functioning? Here are a few recommendations:  

1. We should strive to limit the number of distractions in the classroom. Put smartphones away and out of sight. 
2. If the mode of instruction is primarily a lecture, then tell your students not to take notes during the lecture [2]. Instead, ask that they listen to what you are saying. After class is over, students should then be given a chance to write down everything they remember. I assume this is a controversial recommendation, so expect students to push back.
3. Response suppression and attentional focus are both skills that can be learned. One way to develop these skills is mindfulness training, which is starting to gain some empirical support [4]. 

In summary, executive function is a critical component to higher-order thinking and reasoning. In other words, it definitely deserves the corner office! 

Share and Enjoy!

Dr. Bob

Going Beyond the Information Given

[1] This "game" is a test of executive function because you have to hold in working memory the symbol-to-match. The stimuli were created to be highly confusable; therefore, you must suppress certain responses (e.g., the "d" with only a single dot above it, or a "d" with two dots below it). I heavily borrowed the design from the "d2" test of executive function: Lyons, E. M., Simms, N., Begolli, K. N., & Richland, L. E. (2018). Stereotype threat effects on learning from a cognitively demanding mathematics lesson. Cognitive science, 42(2), 678-690.

[2] The "intuitive" versus "algebraic" answer is a good example of the distinction Daniel Kahneman makes in his book Thinking, Fast and Slow. 

[3] I was fortunate enough to take a course from Herbert A. Simon. He didn't let us take notes during his lectures precisely because we are serial processors. In other words, he applied the findings from cognitive science (a field he helped start!) to his own class. 

[4] Bellinger, D. B., DeCaro, M. S., & Ralston, P. A. (2015). Mindfulness, anxiety, and high-stakes mathematics performance in the laboratory and classroom. Consciousness and cognition, 37, 123-132.

Do or Do Not: The Doer Effect

Learning By Doing

Let's pretend you work for a software company, and your manager wants you to create a clickable prototype for an app you are about to launch. 

Part of your prototype includes a dropdown menu that appears when users hover over it; however, you've never mocked up a dropdown menu before. 

You have two learning paths available to you. Would you rather:

1. Watch a video of someone making a dropdown menu.
2. Find a written worked-out example and follow along with your favorite prototyping software. 

Based on your choice: 

• Which path do you think will be easier to follow in the short term? 
• Which learning path will result in longer-term learning? 
• Which learning path might generalize to other related tasks?

"Do…or do not. There is no try." —Master Yoda, The Empire Strikes Back (1980)

Since the early days of this blog, we've opened with a Learning By Doing activity. What is the point of that? Is there evidence that this is a useful thing to do? 

Before jumping to the data, the idea of "learning by doing" is not at all new. Origins of the idea can be found in quotes by Aristotle [1] and Confucius [2]. John Dewey popularized the idea in American education in his book, Democracy and education [3].

There are theoretical reasons to believe that learning by doing will result in more durable and lasting changes. For example, I remember my memories better than I remember yours. Why? Because our brains are selfish. It is advantageous to our survival to remember the things we've done, both in terms of our successes and mistakes. We can also teach ourselves new strategies for solving problems that we've encountered several times in the past [4].

There are also empirical reasons why we learn better by active engagement. For example, we know from memory research that if we have an active hand in generating items to remember, we have a better shot of remembering them later. This effect goes by the name the generation effect.

If you're in a MOOC, be a Doer!

It seems that "learning by doing" is an effective learning mechanism when we test people in the lab. What does it look like out in the wild? What does the evidence look like in the classroom? 

Fortunately, with the advent of online education, we now have a ready-made venue that offers the opportunity for naturalistic experiments. Many "massive open online courses" (or "MOOCs") offer the learner several different types of learning activities. Most MOOCs have video-based lectures, online textbook passages; some even offer active-learning resources such as computer tutors or simulations. For MOOCs that offer both, which learning activities offer the best learning outcomes? 

Dr. Ken Koedinger and his collaborators conducted a pair of studies to answer precisely this question [5, 6]. They categorized students into several groups, based on their in-class behavior. Students who primarily watched videos were categorized as "Watchers", those who read the text were called "Readers", and those who completed the interactive learning activities were categorized as "Doers". Then the researchers looked at their performance on both quizzes and the final exam. The learning outcomes were extremely consistent. No matter which outcome variable they used, students who were categorized as Doers outperformed the Readers and Watchers. 

To estimate the impact of engaging in more interactive learning resources, they computed a statistical model that looked at the impact of pretest, doing activities, watching videos, or reading text on the final exam grade. The magnitude of the impact of doing the activities was huge. Completing the learning activities was six times more impactful than just watching videos or reading the text. 

This is strong evidence that learning by doing is an effective learning mechanism in online classrooms.

The Classroom Connection

The implication for education is fairly straightforward since the evidence was taken straight from an online course. In fact, their results are completely consistent with the ICAP framework from a previous post. As you move from a passive learning experience (e.g., reading text or watching a video) to more interactive learning environment (e.g., solving a problem or drawing a diagram), then learning tends to improve.

The educational goal, obviously, is to make the "lesson come alive" by actively engaging students in their learning. Active learning can assume an unlimited number of forms. But the point is that you don't want to rely just on asking your students to watch a video. Instead, follow up with a series of questions. Or, better yet, ask them to engage in the same activities as the video (kind of like the standard "I do, we do, you do" sequence). The danger is, if videos (or text) aren't followed up with an activity, then students risk tricking themselves into thinking "they get it."

Thanks for reading. Now go do something! 

Share and Enjoy!

Dr. Bob

Going Beyond the Information Given

[1] “For the things we have to learn before we can do them, we learn by doing them.” 

― Aristotle, The Nicomachean Ethics

[2] I hear and I forget

     I see and I remember

     I do and I understand 

—Confucius

[3] Of course, merely acting does not guarantee learning. There has to a meaningful connection of action to its consequences for there to be any useful learning. Dewey, J. (1923). Democracy and education: An introduction to the philosophy of education. macmillan.

[4] Anzai, Y., & Simon, H. A. (1979). The theory of learning by doing. Psychological review, 86(2), 124.

[5] Koedinger, K. R., Kim, J., Jia, J. Z., McLaughlin, E. A., & Bier, N. L. (2015, March). Learning is not a spectator sport: Doing is better than watching for learning from a MOOC. In Proceedings of the second (2015) ACM conference on learning @ scale (pp. 111-120).

[6] Koedinger, K. R., McLaughlin, E. A., Jia, J. Z., & Bier, N. L. (2016, April). Is the doer effect a causal relationship? How can we tell and why it's important. In Proceedings of the Sixth International Conference on Learning Analytics & Knowledge (pp. 388-397).